Maxima and Minima

Returns the (regular or parallel) maxima and minima of the input values.

pmax*() and pmin*() take one or more vectors as arguments, recycle them to common length and return a single vector giving the ‘parallel’ maxima (or minima) of the argument vectors.

Usage

pmax(..., na.rm = FALSE)

Arguments

...

numeric or character arguments (see Note).

na.rm

a logical indicating whether missing values should be removed.

Value

For min or max, a length-one vector. For pmin or

pmax, a vector of length the longest of the input vectors, or length zero if one of the inputs had zero length.

The type of the result will be that of the highest of the inputs in the hierarchy integer < double < character.

For min and max if there are only numeric inputs and all are empty (after possible removal of NAs), the result is double (Inf or -Inf).

Details

max and min return the maximum or minimum of all the values present in their arguments, as integer if all are logical or integer, as double if all are numeric, and character otherwise.

If na.rm is FALSE an NA value in any of the arguments will cause a value of NA to be returned, otherwise NA values are ignored.

The minimum and maximum of a numeric empty set are +Inf and -Inf (in this order!) which ensures transitivity, e.g., min(x1, min(x2)) == min(x1, x2). For numeric x max(x) == -Inf and min(x) == +Inf whenever length(x) == 0 (after removing missing values if requested). However, pmax and pmin return NA if all the parallel elements are NA even for na.rm = TRUE.

pmax and pmin take one or more vectors (or matrices) as arguments and return a single vector giving the ‘parallel’ maxima (or minima) of the vectors. The first element of the result is the maximum (minimum) of the first elements of all the arguments, the second element of the result is the maximum (minimum) of the second elements of all the arguments and so on. Shorter inputs (of non-zero length) are recycled if necessary. Attributes (see attributes: such as names or dim) are copied from the first argument (if applicable, e.g., not for an S4 object).

pmax.int and pmin.int are faster internal versions only used when all arguments are atomic vectors and there are no classes: they drop all attributes. (Note that all versions fail for raw and complex vectors since these have no ordering.)

max and min are generic functions: methods can be defined for them individually or via the Summary group generic. For this to work properly, the arguments ... should be unnamed, and dispatch is on the first argument.

By definition the min/max of a numeric vector containing an NaN is NaN, except that the min/max of any vector containing an NA is NA even if it also contains an NaN. Note that max(NA, Inf) == NA even though the maximum would be Inf whatever the missing value actually is.

Character versions are sorted lexicographically, and this depends on the collating sequence of the locale in use: the help for ‘Comparison’ gives details. The max/min of an empty character vector is defined to be character NA. (One could argue that as "" is the smallest character element, the maximum should be "", but there is no obvious candidate for the minimum.)

Note

‘Numeric’ arguments are vectors of type integer and numeric, and logical (coerced to integer). For historical reasons, NULL is accepted as equivalent to integer(0).

pmax and pmin will also work on classed S3 or S4 objects with appropriate methods for comparison, is.na and rep (if recycling of arguments is needed).

S4 methods

max and min are part of the S4 Summary group generic. Methods for them must use the signature x, ..., na.rm.

References

Becker, R. A., Chambers, J. M. and Wilks, A. R. (1988) The New S Language. Wadsworth & Brooks/Cole.

See also

range (both min and max) and which.min (which.max) for the arg min, i.e., the location where an extreme value occurs.

‘plotmath’ for the use of min in plot annotation.

Examples

require(stats); require(graphics)
 min(5:1, pi) #-> one number
#> [1] 1
pmin(5:1, pi) #->  5  numbers
#> [1] 3.141593 3.141593 3.000000 2.000000 1.000000

x <- sort(rnorm(100));  cH <- 1.35
pmin(cH, quantile(x)) # no names
#> [1] -2.61233433 -0.35607619  0.09103647  0.62341005  1.35000000
pmin(quantile(x), cH) # has names
#>          0%         25%         50%         75%        100% 
#> -2.61233433 -0.35607619  0.09103647  0.62341005  1.35000000 
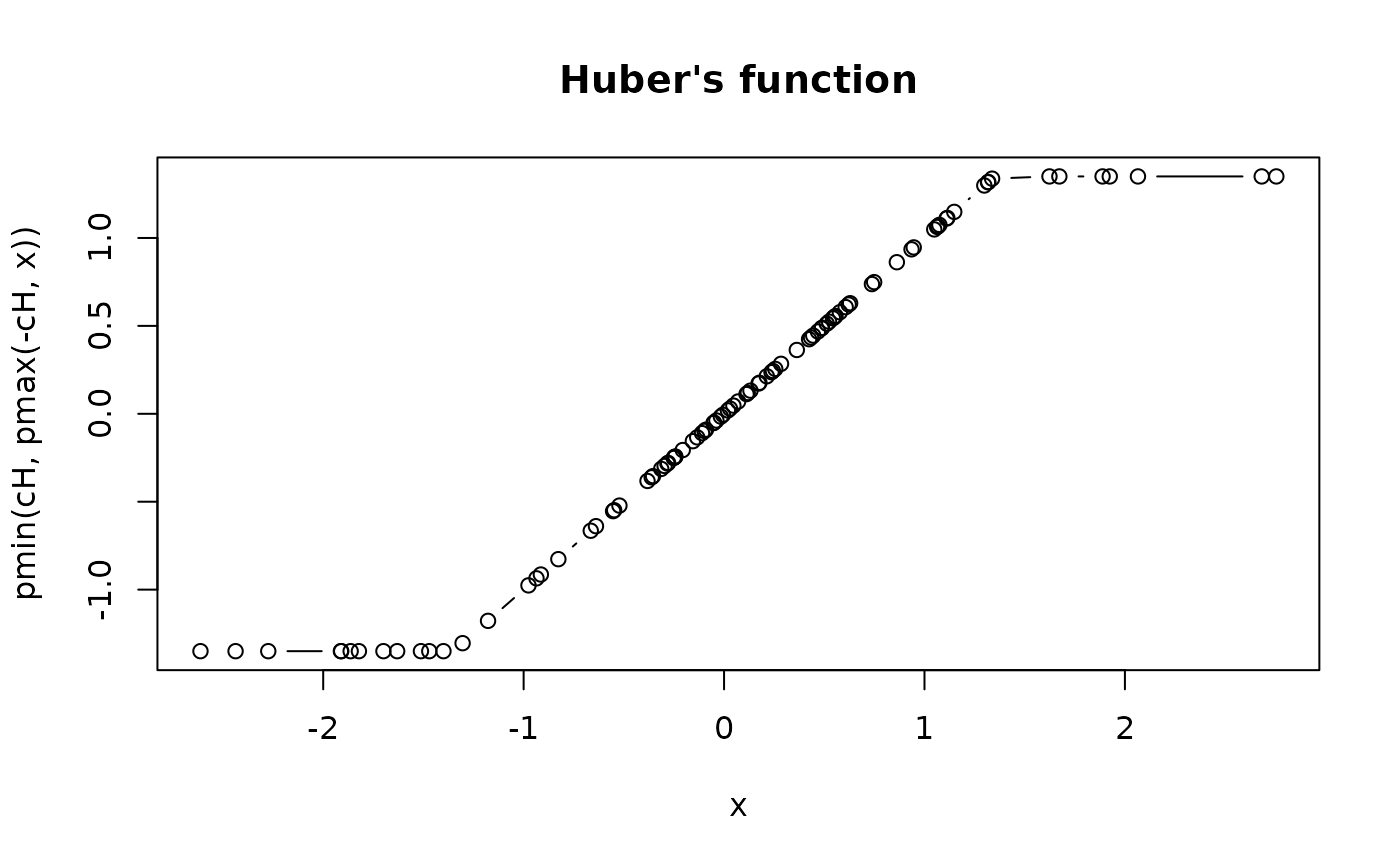
plot(x, pmin(cH, pmax(-cH, x)), type = "b", main =  "Huber's function")


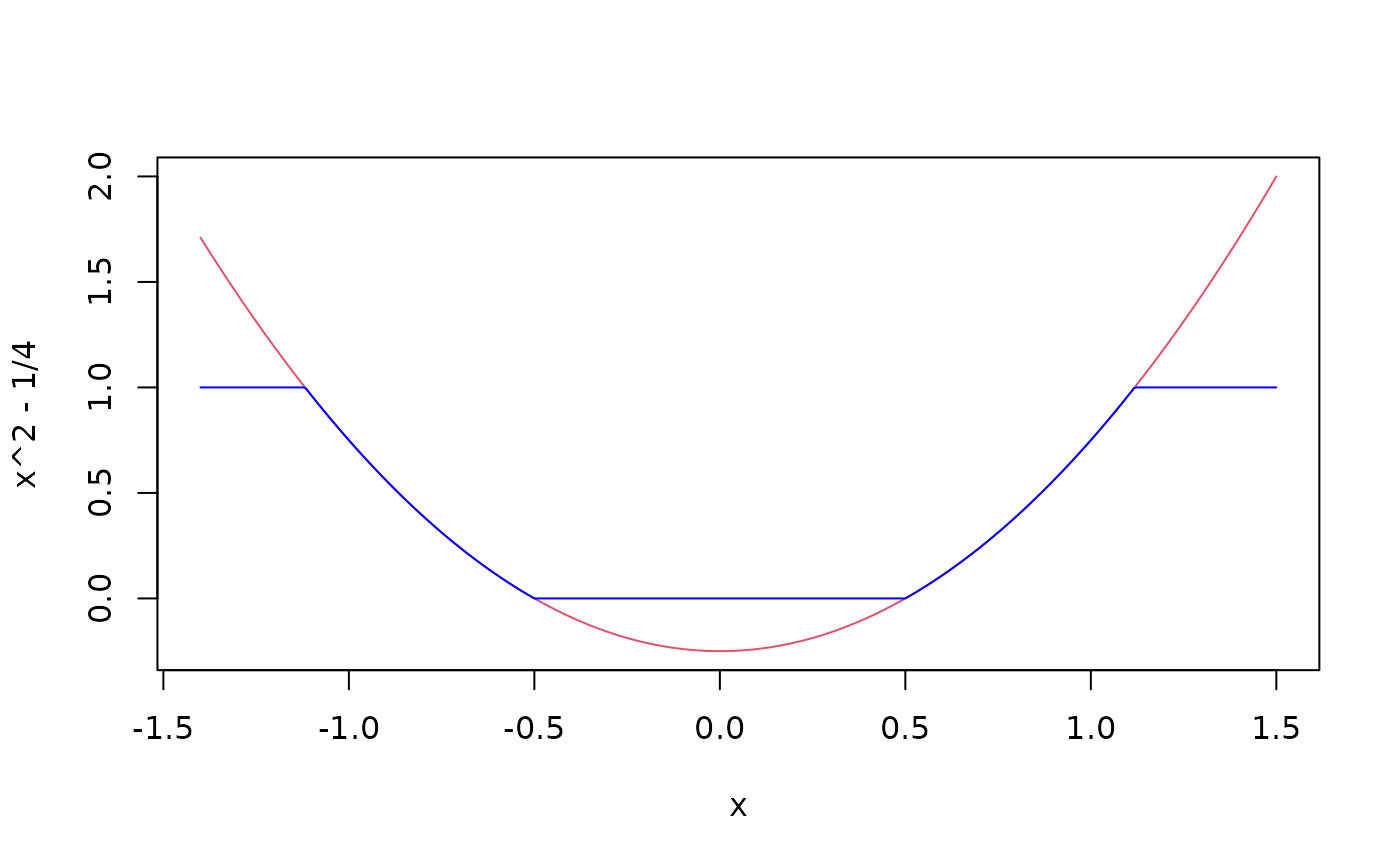
cut01 <- function(x) pmax(pmin(x, 1), 0)
curve(      x^2 - 1/4, -1.4, 1.5, col = 2)
curve(cut01(x^2 - 1/4), col = "blue", add = TRUE, n = 500)

## pmax(), pmin() preserve attributes of *first* argument
D <- diag(x = (3:1)/4) ; n0 <- numeric()
stopifnot(identical(D,  cut01(D) ),
          identical(n0, cut01(n0)),
          identical(n0, cut01(NULL)),
          identical(n0, pmax(3:1, n0, 2)),
          identical(n0, pmax(n0, 4)))